DistilQwen2.5-R1发布:知识蒸馏助推小模型深度思考
作者:蔡文睿(清素)、汪诚愚(熊兮)、严俊冰(玖烛)、黄俊(临在)
引言
随着 DeepSeek-R1 和 QwQ-32B 等面向深度推理的大语言模型的开源,“大模型+慢思考”已成为拓展大语言模型智能边界的标准配置。然而,这些模型在资源受限的移动设备和边缘计算场景中的普及仍面临巨大挑战。因此,学术界和工业界迫切需要解决如何有效利用知识蒸馏技术,将这些超大规模深度推理模型的知识迁移到小模型中,从而提升计算效率并降低部署成本的问题。为此,我们在 DistilQwen2.5 系列蒸馏小模型(看这里)的基础上,推出了更为强大的 DistilQwen2.5-R1 系列深度推理模型。
DistilQwen2.5-R1 系列以少量来自 DeepSeek-R1 的思维链蒸馏数据为基础,通过一系列创新的蒸馏策略,有效强化了小模型的深度思考能力。实验评估结果显示,DistilQwen2.5-R1 系列中的多种小规模模型在各项基准测试中表现优异(见下图)。例如,DistilQwen2.5-R1-7B 性能显著超越了其他开源蒸馏模型,包括 OpenThinker-7B。


为方便开发者和企业在实际应用中使用 DistilQwen2.5-R1 系列模型,其所有的 Checkpoint 已在 Hugging Face 和 Model Scope 开源社区中公开。本文将深入阐述 DistilQwen2.5-R1 的蒸馏算法、性能评估,并且提供在阿里云人工智能平台 PAI 上的使用指南及相关下载教程。
DistilQwen2.5-R1中的知识蒸馏技术
本节中,我们主要描述 DistilQwen2.5-R1 模型训练中使用的数据增强与知识蒸馏技术。
由于自身参数量的显著差异,大模型与小模型的认知与推理轨迹有时并不完全一致。以数学问题为例:对于有的数学问题,小模型由于自身参数量的限制,会倾向于使用更基础的方法去解决问题。而大模型基于其强大的推理能力,会采用较为高阶的方法。比如经典的鸡兔同笼问题,小模型倾向于使用简单枚举法逐一试错,而大模型会直接通过列方程的较高级方法求解。
正是由于大小模型的认知轨迹偏差,小模型有时无法有效理解大模型的思维链,此时如果直接该思维链(Chain-of-Thought,CoT)蒸馏到小模型中,往往效果不佳。为此,我们设计了一种小型推理模型训练框架,以消除这种认知轨迹偏差带来的负面影响。在后续训练中,我们还利用这种偏差数据进一步提升小模型的推理能力,最终推出基于该训练框架的 DistilQwen2.5-R1 系列模型。我们提出的训练技术框架包含两个阶段:CoT 数据“评价-改进-验证”机制,以及基于不同认知轨迹数据的偏好优化算法。总体而言,DistilQwen2.5-R1 模型蒸馏的详细算法框架如下图所示:

给定原始的大模型思维链数据集,例如从 DeepSeek-R1 蒸馏的数据集,在一阶段,我们先对其进行数据难度评价,接着根据数据的难度等级对其进行相应的优化,优化之后还要对结果进行验证。我们使用改进且被验证的 CoT 数据集对模型进行 SFT 训练,获取模型的基础推理能力。在二阶段,我们利用一阶段已有的不同难度的 CoT 数据构造偏好数据集,在一阶段的基础上进一步提升小模型的推理能力。
CoT 数据“评价-改进-验证”机制
正如上文中提到的,大小模型间的认知推理轨迹有时存在显著偏差。因此,对于待蒸馏的大模型思维链数据集,小模型无法完全理解。阶段一正是基于这种认知偏差对数据集进行优化,采用了 LLM-as-a-Judge 的范式,对大模型的推理过程进行评价并改进。
给定问题、大模型的推理过程和问题的答案,我们使用模型判断这个推理过程是简单、中等还是困难。难度等级的核心标准是小模型是否能够遵循给定的推理过程得到问题的答案。以下是思维链的难度等级及定义:
· 中等: 小模型可以遵循该推理过程得到问题的答案。
· 简单: 给定的推理过程过于简单,缺少小模型所需的必要步骤,导致大模型依赖其强大的推理能力解决问题,而小模型无法遵循该过程得到答案。
· 困难: 给定的推理过程过于复杂或过于困难,导致小模型无法遵循该过程得到答案。
基于一个大模型的问题与思维链集合,我们可以将其分为简单、中等和困难三类。对于评级为中等的部分,我们予以保留。对于被评为简单和困难的数据,我们使用模型对思维链进行改进。具体来说:对于简单部分,我们扩展其推理过程,直至小模型可以遵循扩展的过程得到答案。对于评级为困难的部分,我们精简其推理过程,直至小模型可以遵循精简的过程得到答案。
我们之后对改进结果进行进一步验证,包括:对改进后的思维链再次评价难度等级,检测其是否被归类为中等难度,以及验证小模型是否能够遵循改进的思维链解决问题。如果改进后的思维链通过验证,说明改进有效,该数据可以被小模型有效理解,我们将其保留。如果验证不通过,说明改进无效,我们将返回到改进步骤,重新进行改进,直至通过验证。最终,我们获取了优化后的思维链数据集,其组成部分如下:
· 初始难度评级为中等的数据。
· 初始难度评级为简单,经过改进扩展后评为中等并通过验证的数据。
· 初始难度评级为困难,经过改进精简后评为中等并通过验证的数据。
此时,数据集内所有思维链的最终难度评级均为中等,意味着小模型可以有效理解数据集内的所有思维链,并能遵循这些思维链解决相应推理问题。上文提到的大小模型认知轨迹偏差问题在改进后的数据集中得到妥善解决,其可能带来的负面影响也被消除。我们使用优化后的思维链数据集对 Qwen2.5 系列基座模型进行监督微调(SFT),得到 DistilQwen2.5-R1 系列模型的基础结果。
基于多种认知轨迹数据的偏好优化
在第二阶段,我们基于第一阶段得到的不同难度等级数据对模型进行进一步提升。
具体来说,在第一阶段中,评级难度为中等的思维链数据是正确且适合小模型的思维链,小模型能够有效理解该思维链并解决问题。而难度评级为简单或困难的思维链数据依然是正确的思维链,只是不适合小模型。在此基础上,我们使用模型将正确的推理过程改写为一个错误的推理过程。错误的推理过程没有逻辑性,且会误导小模型,使得小模型完全无法遵循该错误的推理过程解决问题。
基于改写得到的错误思维链,我们将其与简单、中等和困难的思维链进行两两组合,组成多种偏好数据对。这些偏好数据对中有的偏差大,有的偏差小。基于不同种类的偏好数据对及其特点,我们分别使用针对性的参数配置,在第一阶段模型的基础上,采用 DPO 算法进一步优化小模型的推理能力。
最终,我们利用第一阶段得到的不同难度等级的认知轨迹(思维链)数据以及基础模型结果,得到了 DistilQwen2.5-R1 系列模型。
DistilQwen2.5-R1 模型效果评测
在本节中,我们从多个角度评测 DistilQwen2.5-R1 系列蒸馏小模型的实际效果;同时,我们将 DistilQwen2.5-R1 系列模型和当前业界的前沿模型对比效果。
模型综合能力评测
我们在多个模型推理能力评测基准上测试了 DistilQwen2.5-R1 系列模型的能力,涵盖数学、代码和科学问题三个主流推理领域。
在数学领域,我们使用 AIME2024 和 MATH-500 这两个基准进行测试,AIME2024 是美国数学邀请赛的2024年测试集,包含30道高难度数学题,用于评估大语言模型在复杂数学推理和问题解决能力,尤其考察代数、几何等领域的综合应用。MATH-500 是一个数学推理能力的基准测试,包含500个测试样本,旨在全面考察模型在数学解题上的能力。它与 AIME2024 类似,但有其独特的测试目标和对比结果,用于衡量模型在不同数学题目上的准确性。
在代码领域,我们使用 LiveCodeBench 基准,LiveCodeBench 是一个动态更新的基准测试平台,用于全面评估大型语言模型在复杂编码场景中的能力。它通过从顶级竞赛平台收集高难度编程任务来测试模型的代码生成、自我修复代码执行和测试等能力,是一个综合性、无污染的评价基准。在本次评测中,我们使用 LiveCodeBench 基准的V2版本,其包含2023年5月-2024年5月的511个代码问题。
在科学问题领域,我们使用 GPQA-Diamond(Grade-Level Problems in Question Answering Diamond)基准,其由纽约大学、CohereAI 及 Anthropic 的研究人员联合发布,包含198条结果,是 GPQA 系列中最高质量的评测数据,用于评估模型解决专家级科学问题的能力。
如下图所示,DistilQwen2.5-R1 系列模型在3B、7B、14B和32B四个参数量级的模型中,与原始 Qwen2.5 模型的效果进行了对比。可以看出,本文描述的小型推理模型训练框架显著提升了现有语言模型的推理能力,并在多个评测基准上取得了一致而明显的效果提升。
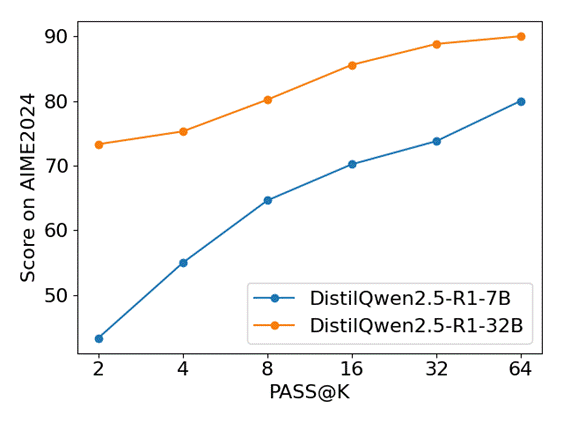
AIME2024实验结果对比:

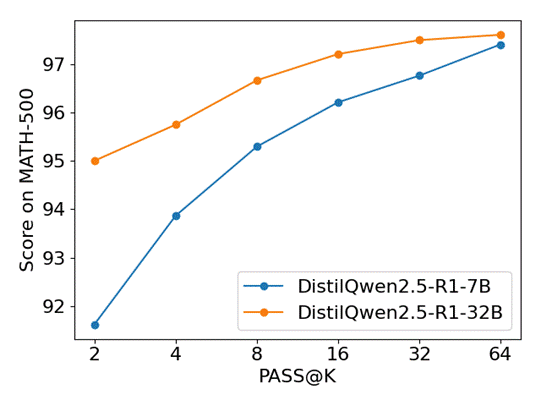
MATH-500实验结果对比:
 |
|
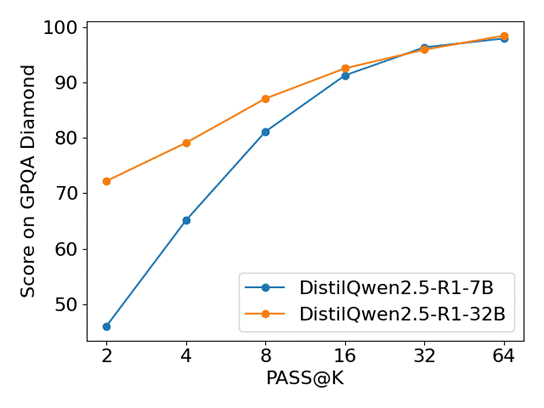
GPQA Diamond实验结果对比:

LiveCodeBench V2实验结果对比:
 |
|
与其他模型能力对比
为了横向比较同期发布的不同参数规模的推理模型效果,下表分别是 DistilQwen2.5-R1 系列模型在各个参数量级上与其他前沿推理模型在上文提到的4个基准的评测结果。我们重点对比了 DistilQwen2.5-R1 系列与 OpenThinker、DeepSeek-R1-Distill-Qwen等系列模型。
以下是7B量级的对比结果,可以看出,DistilQwen2.5-R1-7B 模型超越了 Bespoke-Stratos-7B 和 OpenThinker-7B。值得注意的是,相较于 OpenThinker-7B,DistilQwen2.5-R1-7B 在使用更少训练数据的情况下在所有基准上达到了更高的结果。DeepSeek-R1-Distill-Qwen-7B 使用了800k闭源训练数据,而 DistilQwen2.5-R1-7B 使用了开源数据进行训练(OpenThoughts数据集过滤和改写得到的子集),在基于开源数据模型领域内处于领先地位。
| 模型 |
训练数据量 |
AIME2024 |
MATH-500 |
GPQA Diamond |
LiveCodeBench V2 |
| DeepSeek-R1-Distill-Qwen-7B (reported) |
800k |
55.5 |
92.8 |
49.1 |
- |
| Bespoke-Stratos-7B (reported) |
17k |
20.0 |
82.0 |
37.8 |
36.1 |
| OpenThinker-7B (reported) |
114k |
31.3 |
83.0 |
42.4 |
39.9 |
| DistilQwen2.5-R1-7B |
105k |
43.33 |
88.4 |
42.93 |
46.38 |
以下是32B量级的对比结果。同样地,DistilQwen2.5-R1-32B 在所有已知基准上超越了 Sky-T1-32B-Preview,以及在绝大多数基准上超越了 OpenThinker-32B。
| 模型 |
训练数据量 |
AIME2024 |
MATH-500 |
GPQA Diamond |
LiveCodeBench V2 |
| DeepSeek-R1-Distill-Qwen-32B (reported) |
800k |
72.6 |
94.3 |
62.1 |
- |
| Sky-T1-32B-Preview (reported) |
17k |
43.3 |
86.4 |
56.8 |
- |
| OpenThinker-32B (reported) |
114k |
66.0 |
90.6 |
61.6 |
68.9 |
| DistilQwen2.5-R1-32B |
105k |
70.0 |
93.8 |
62.12 |
65.95 |
模型多次推理评测
我们还测试了 DistilQwen2.5-R1 系列模型在上文提到的四个基准上多次推理的结果,模型会对同一个问题生成k个回答进行评测,即 Pass@k 指标。以下是 DistilQwen2.5-R1-7B 和 DistilQwen2.5-R1-32B 在四个基准上Pass@k结果(k=2、4、8、16、32、64)。
可以看出,随着模型推理次数k的逐步增加,两个模型在所有基准上的评测准确率大幅提高。值得注意的是,随着k的增加,DistilQwen2.5-R1-7B 在 MATH-500和GPQA-Diamond 上涨幅巨大,并且不断逼近 DistilQwen2.5-R1-32B 水准。这表明我们的推理模型训练框架在小模型领域内拥有巨大潜力。我们可以通过多次推理的方式使7B模型拥有媲美32B模型的能力,极大减少了推理所需的计算资源。
模型输出案例
对同一数学问题,我们对比了 DistilQwen2.5-R1 系列模型在7B、32B量级和同等量级模型的推理结果。从输出结果可以看出,DistilQwen2.5-R1 系列模型在同量级推理模型中处于领先地位。
示例一:7B量级模型对比
| 问题 |
Peter has $70 and wishes to spend an equal amount each day for one week. From Sunday through Wednesday, he spent his money on wooden action figures which cost $5 each. For the rest of the week, he will buy plastic action figures which cost $2 each. How many total action figures will he have by the end of the week? |
| 答案 |
There are 7 days in a week so if he wishes to spend an equal amount of $70 each day that would be $70/7 = $<<70/7=10>>10\nFor four days (Sunday through Wednesday) he will spend 4*$10 = $<<4*10=40>>40\nHe will spend $40 on wooden action figures of $5 each which gives $40/$5 = <<40/5=8>>8 wooden action figures\nFor the remaining 3 days he will spend 3*$10 = $<<3*10=30>>30\nHe will spend $30 on plastic action figures of $2 each which gives $30/$2 = <<30/2=15>>15 plastic action figures\nAltogether, he will have 8+15 = <<8+15=23>>23 action figures.\n#### 23 |
| DistilQwen2.5-R1-7B |
<|begin_of_thought|>
Okay, let's try to figure out how many action figures Peter can buy. First, I need to understand the problem step by step.
So, Peter has $70 and wants to spend an equal amount each day for one week. That means seven days total. From Sunday through Wednesday, he spends money on wooden action figures that cost $5 each. Then, for the rest of the week (which would be Thursday and Friday, I guess, since the week ends on Saturday or Sunday?), he buys plastic ones that cost $2 each. The question is asking how many total action figures he'll have by the end of the week.
Wait, the problem says "from Sunday through Wednesday," so that's four days. Then "for the rest of the week," which would be Thursday and Friday, making two days. So total days: 4 + 2 = 6 days? Wait, a week is seven days. If he's spending from Sunday through Wednesday (4 days), then the rest would be Thursday and Friday (2 days), but that's only 6 days. Wait, maybe the "rest of the week" includes Saturday as well? Because Sunday to Wednesday is four days, then Thursday to Saturday would be three days left. Hmm, maybe I need to clarify that.
Wait, the problem says "for the rest of the week," which could be interpreted differently. Let me check again. The problem states: "From Sunday through Wednesday, he spent his money on wooden action figures..." So that's four days. Then "For the rest of the week, he will buy plastic action figures which cost $2 each." So "rest of the week" would be the remaining days of the week after Sunday through Wednesday. Since Sunday is the first day, the week would be Sunday, Monday, Tuesday, Wednesday, Thursday, Friday, Saturday. So from Sunday to Wednesday is four days. The rest would be Thursday, Friday, Saturday. That's three days. So total days: 4 + 3 = 7 days, which is a week. Okay, so that makes sense.
So he spends four days on wooden figures ($5 each) and three days on plastic ones ($2 each). The total amount he spends is $70, and he wants to spend an equal amount each day. So first, we need to figure out how much he spends each day, then calculate how many action figures he can buy each day, and sum them up.
Wait, but the problem says he has $70 and wishes to spend an equal amount each day for one week. So the total amount he spends is $70, divided equally over seven days. So each day he spends $70 / 7 = $10 per day. So $10 per day total for the week.
But then, from Sunday through Wednesday (four days), he spends on wooden figures ($5 each), and the remaining three days (Thursday, Friday, Saturday) he spends on plastic figures ($2 each). So the total amount he spends on wooden figures is 4 days * $10/day = $40. Then the remaining amount is $70 - $40 = $30, which he spends over three days at $2 each. So $30 / 3 days = $10 per day, which matches the total daily spending of $10. So that checks out.
Now, how many wooden action figures does he buy? Each costs $5, and he spends $10 on them each day for four days. Wait, but if each day he spends $10 on wooden figures, then each day he can buy $10 / $5 = 2 action figures per day. So over four days, that's 2 * 4 = 8 wooden action figures.
Then, for the plastic figures, he spends $10 per day for three days. Each plastic figure is $2, so per day he can buy $10 / $2 = 5 action figures per day. Over three days, that's 5 * 3 = 15 plastic action figures.
Total action figures: 8 + 15 = 23.
Wait, but let me verify this again. Let's check the total money spent. Wooden: 8 figures * $5 = $40. Plastic: 15 figures * $2 = $30. Total: $40 + $30 = $70. Which matches the total he has. So that's correct.
Alternatively, another way to look at it: since he spends $10 each day, total $70 over 7 days. So each day he spends $10. For the first four days, he uses $10 each day on $5 action figures. So each day, $10 / $5 = 2 per day. 4 days: 8. Then the remaining three days, $10 each day on $2 action figures: $10 / $2 = 5 per day. 3 days: 15. Total 23.
Yes, that seems to be the answer.
<|end_of_thought|>
<|begin_of_solution|>
Peter has $70 to spend over 7 days. He spends $10 each day ($70 ÷ 7 = $10/day).
**Wooden action figures (Sunday–Wednesday, 4 days):**
Each costs $5. Daily purchase: $10 ÷ $5 = 2 figures/day.
Total: 2 × 4 = **8 figures**.
**Plastic action figures (Thursday–Saturday, 3 days):**
Each costs $2. Daily purchase: $10 ÷ $2 = 5 figures/day.
Total: 5 × 3 = **15 figures**.
**Total action figures:**
8 (wooden) + 15 (plastic) = **23**.
\boxed{23}
<|end_of_solution|> |
| DeepSeek-R1-Distill-Qwen-7B |
Okay, let's see. Peter has $70 and wants to spend an equal amount each day for one week. So first, I need to figure out how much he spends each day. A week has seven days, right? From Sunday through Wednesday, he buys wooden action figures that cost $5 each. Then, for the rest of the week, which would be Thursday and Friday, he buys plastic ones that cost $2 each. The question is asking how many total action figures he'll have by the end of the week.
Wait, hold on. Wait, a week is seven days. Sunday through Wednesday is four days, and then the rest is Thursday and Friday, that's two days. So total of six days? Wait, Sunday, Monday, Tuesday, Wednesday is four days. Then Thursday and Friday, that's two days. So total of six days he's spending money, leaving Saturday out? The problem says "for one week," so maybe he starts on Sunday and goes through Saturday? But the problem mentions spending from Sunday through Wednesday, and then the rest of the week. Hmm.
Wait, the problem says: "From Sunday through Wednesday, he spent his money on wooden action figures which cost $5 each. For the rest of the week, he will buy plastic action figures which cost $2 each." So Sunday to Wednesday is four days, then the rest of the week would be Thursday to Saturday, which is three days. Wait, that's three days. So total of seven days? Wait, no. Sunday to Saturday is a week. If Sunday through Wednesday is four days, then the remaining days are Thursday, Friday, Saturday, which is three days. So total of seven days. So he spends money on four days buying wooden figures and three days buying plastic ones.
But the problem says he spends an equal amount each day for one week. So total spending per day is consistent. So first, I need to find out how much he spends each day. Let me denote the daily amount as x dollars. So total spending for the week would be 7x because it's one week. But he has $70. So 7x = $70. Therefore, x = 10. So he spends $10 each day.
Wait, but that seems high. Let me check. If he spends $10 each day for seven days, that's $70 total. That makes sense. So each day he spends $10. Then, from Sunday through Wednesday, which is four days, he spends 4 days * $10/day = $40 on wooden action figures. Then, for the rest of the week, which is three days (Thursday, Friday, Saturday), he spends 3 days * $10/day = $30 on plastic action figures. So total $40 + $30 = $70, which matches his total money. That checks out.
Now, the problem is asking for the total number of action figures he will have by the end of the week. So we need to calculate how many wooden figures he bought during the four days and how many plastic figures he bought during the three days, then sum them up.
First, wooden action figures cost $5 each. He spent $40 on them. So the number of wooden figures is $40 divided by $5 per figure. That's 40 / 5 = 8 figures.
Then, plastic action figures cost $2 each. He spent $30 on them. So the number of plastic figures is $30 divided by $2 per figure. That's 30 / 2 = 15 figures.
Adding them together: 8 wooden + 15 plastic = 23 total action figures.
Wait a second, but let me verify again to make sure I didn't make a mistake. So total days are seven. He spends $10 each day. Total $70. From Sunday to Wednesday: four days. 4 days * $10 = $40. Then Thursday, Friday, Saturday: three days * $10 = $30. Correct. Then wooden figures: $40 / $5 = 8. Plastic: $30 / $2 = 15. Total 23. That seems right.
But wait, the problem says "for the rest of the week, he will buy plastic action figures which cost $2 each." So does "rest of the week" mean the remaining days after Sunday through Wednesday? Sunday through Wednesday is four days, so the remaining three days would be Thursday, Friday, Saturday. So three days. So three days of $10 each day, totaling $30. Correct.
Therefore, the total number of action figures is 8 + 15 = 23. So the answer is 23.
Peter spends $10 each day for 7 days, totaling $70. From Sunday to Wednesday (4 days), he buys wooden action figures at $5 each:
\[
\frac{4 \text{ days} \times \$10}{\$5/\text{figure}} = \frac{\$40}{\$5} = 8 \text{ figures}.
\]
For the remaining 3 days (Thursday to Saturday), he buys plastic action figures at $2 each:
\[
\frac{3 \text{ days} \times \$10}{\$2/\text{figure}} = \frac{\$30}{\$2} = 15 \text{ figures}.
\]
Total action figures:
\[
8 + 15 = \boxed{23}.
\] |
示例二:32B量级模型对比
| 问题 |
A shoe store was having a weekend sale on a brand of popular tennis shoes. On Friday the store sold 14 pairs of tennis shoes. The next day they sold double that number of shoes. On the last day of the sale they sold one-half the amount that they did the day before, but six people returned their pairs because they didn't fit. How many pairs of tennis shoes were sold by the end of the sale? |
| 答案 |
On Saturday 14*2=<<14*2=28>>28 shoes were sold\nOn Sunday 28/2=<<28/2=14>>14 shoes were sold\nBefore the returns were made 14+28+14=<<14+28+14=56>>56 pairs of shoes were sold\nAfter the returns were made 56-6=<<56-6=50>>50 pairs of shoe were sold\n#### 50 |
| DistilQwen2.5-R1-32B 回复 |
<|begin_of_thought|>
Okay, let me try to figure out this problem step by step. So, the shoe store had a sale on tennis shoes over the weekend. Let's break down the information given.
First, on Friday, they sold 14 pairs of tennis shoes. That's straightforward. Then, the next day, which would be Saturday, they sold double that number. Double of 14 is 28, right? So, 28 pairs on Saturday.
Then, on the last day of the sale, which is Sunday, they sold half the amount they did the day before. The day before Sunday is Saturday, so half of 28 is 14. So, 14 pairs on Sunday. But wait, there's a catch here. Six people returned their pairs because the shoes didn't fit. So, we need to subtract those 6 returned pairs from the Sunday sales. That means instead of 14, they effectively sold 14 minus 6, which is 8 pairs on Sunday.
Now, to find the total number of tennis shoes sold by the end of the sale, we need to add up the sales from Friday, Saturday, and Sunday, taking into account the returns on Sunday.
So, Friday: 14 pairs.
Saturday: 28 pairs.
Sunday: 14 - 6 = 8 pairs.
Adding those together: 14 + 28 + 8.
Let me calculate that. 14 plus 28 is 42, and then 42 plus 8 is 50. So, total pairs sold would be 50.
Wait, but let me double-check to make sure I didn't make a mistake. Let's verify each step again.
Friday: 14 pairs. Correct. Saturday is double, so 14*2=28. Correct. Sunday is half of Saturday's sales, which is 28/2=14. But then subtract the 6 returned pairs. So 14-6=8. Then total is 14+28+8=50. Yeah, that seems right.
Hmm, another way to look at it: Total sold without returns would be 14 + 28 +14 = 56. Then subtract the 6 returned pairs, which would be 56 -6=50. Same result. So, that confirms it.
I think that's all. So the final answer should be 50 pairs of tennis shoes sold.
<|end_of_thought|>
<|begin_of_solution|>
The shoe store sold 14 pairs on Friday. On Saturday, they sold double that number, which is \(14 \times 2 = 28\) pairs. On Sunday, they sold half of Saturday's sales, which is \(28 \div 2 = 14\) pairs, but then subtract the 6 pairs returned. Therefore, the effective sales on Sunday are \(14 - 6 = 8\) pairs.
Adding up the sales from all three days:
\(14\) (Friday) + \(28\) (Saturday) + \(8\) (Sunday) = \(14 + 28 + 8 = 50\).
The final answer is \(\boxed{50}\).
<|end_of_solution|> |
| DeepSeek-R1-Distill-Qwen-32B 回复 |
Okay, let's try to figure out how many tennis shoes were sold by the end of the sale. So, the problem is about a shoe store that had a weekend sale. I'll need to break it down day by day to make sure I understand each part correctly.
First, on Friday, the store sold 14 pairs of tennis shoes. That seems straightforward. So, Friday sales are 14 pairs.
Next, the problem says that on the next day, which would be Saturday, they sold double that number. Hmm, double of Friday's sales. So, double of 14 is 14 times 2. Let me calculate that: 14 * 2 = 28. So, they sold 28 pairs on Saturday.
Now, moving on to the last day of the sale, which is Sunday. The problem states that on Sunday, they sold half the amount they did the day before. The day before Sunday is Saturday, so half of Saturday's sales. Saturday was 28 pairs, so half of that would be 28 / 2. Let me do that math: 28 divided by 2 is 14. So, they sold 14 pairs on Sunday before any returns.
But wait, the problem mentions that six people returned their pairs because they didn't fit. So, we need to subtract those returns from Sunday's sales. So, Sunday's total after returns would be 14 minus 6. Let me calculate that: 14 - 6 = 8. So, they effectively sold 8 pairs on Sunday after the returns.
Now, to find the total number of pairs sold by the end of the sale, I need to add up the sales from each day. That would be Friday's 14, plus Saturday's 28, plus Sunday's 8. Let me add them up step by step.
First, 14 (Friday) + 28 (Saturday) = 42. Then, adding Sunday's 8 to that: 42 + 8 = 50.
Wait, does that make sense? Let me double-check each step to make sure I didn't make a mistake. Friday was 14, Saturday was 28, Sunday was 14 before returns, which became 8 after subtracting 6. So, 14 + 28 is indeed 42, and 42 + 8 is 50. Yeah, that seems correct.
But just to be thorough, maybe I should think about whether the returns affect the total sold or just the net sales. The problem says "they sold one-half the amount that they did the day before, but six people returned their pairs." So, I think the six returns are subtracted from Sunday's sales, so the total sold would be the initial sales minus the returns. Therefore, the calculation I did is correct.
So, adding all three days together: 14 + 28 + (14 - 6) = 14 + 28 + 8 = 50. Yep, that looks right.
The total number of pairs sold by the end of the sale is 50.
The final answer is 50. |
模型下载和使用
DistilQwen2.5-R1 在阿里云人工智能平台 PAI 上的实践
以下 HuggingFace transformers 库为例,简要介绍如何在 PAI-DSW 上使用 DistilQwen2.5-R1 模型。首先需要保证 PAI-DSW 镜像内 transformers 版本大于等于4.37.0,否则会在加载模型时报错:
KeyError: 'qwen2'
以 DistilQwen2.5-R1-7B 为例,我们可以使用如下代码调用模型:
from transformers import AutoModelForCausalLM, AutoTokenizer
model_name = "alibaba-pai/DistilQwen2.5-R1-7B"
model = AutoModelForCausalLM.from_pretrained(model_name)
tokenizer = AutoTokenizer.from_pretrained(model_name)
prompt = "xxxxx"
messages=[
{"role": "system", "content": "Your role as an assistant involves thoroughly exploring questions through a systematic long thinking process before providing the final precise and accurate solutions. This requires engaging in a comprehensive cycle of analysis, summarizing, exploration, reassessment, reflection, backtracing, and iteration to develop well-considered thinking process. Please structure your response into two main sections: Thought and Solution. In the Thought section, detail your reasoning process using the specified format: <|begin_of_thought|> {thought with steps separated with '\n\n'} <|end_of_thought|> Each step should include detailed considerations such as analisying questions, summarizing relevant findings, brainstorming new ideas, verifying the accuracy of the current steps, refining any errors, and revisiting previous steps. In the Solution section, based on various attempts, explorations, and reflections from the Thought section, systematically present the final solution that you deem correct. The solution should remain a logical, accurate, concise expression style and detail necessary step needed to reach the conclusion, formatted as follows: <|begin_of_solution|> {final formatted, precise, and clear solution} <|end_of_solution|> Now, try to solve the following question through the above guidelines:"},
{"role": "user", "content": prompt},
]
text = tokenizer.apply_chat_template(
messages,
tokenize=False,
add_generation_prompt=True
)
model_inputs = tokenizer([text], return_tensors="pt").to(model.device)
generated_ids = model.generate(
**model_inputs,
max_new_tokens=512
)
generated_ids = [
output_ids[len(input_ids):] for input_ids, output_ids in zip(model_inputs.input_ids, generated_ids)
]
response = tokenizer.batch_decode(generated_ids, skip_special_tokens=True)[0]
print(response)
DistilQwen2.5-R1在开源社区的下载
我们在 Hugging Face 和 Model Scope 上开源了我们蒸馏后的模型,分别为DistilQwen2.5-R1-3B、DistilQwen2.5-R1-7B、DistilQwen2.5-R1-14B、DistilQwen2.5-R1-32B。以Hugging Face为例,用户可以使用如下代码下载这两个模型:
from huggingface_hub import snapshot_download
model_name = "alibaba-pai/DistilQwen2.5-R1-3B"
snapshot_download(repo_id=model_name, cache_dir="./DistilQwen2.5-R1-3B/")
model_name = "alibaba-pai/DistilQwen2.5-R1-7B"
snapshot_download(repo_id=model_name, cache_dir="./DistilQwen2.5-R1-7B/")
model_name = "alibaba-pai/DistilQwen2.5-R1-14B"
snapshot_download(repo_id=model_name, cache_dir="./DistilQwen2.5-R1-14B/")
model_name = "alibaba-pai/DistilQwen2.5-R1-32B"
snapshot_download(repo_id=model_name, cache_dir="./DistilQwen2.5-R1-32B/")
小结与未来工作
本文介绍了 DistilQwen2.5-R1 系列深度推理模型,它在少量来自 DeepSeek-R1 的思维链数据基础上,通过创新蒸馏策略增强了小模型的深度思考能力。实验结果表明,该系列模型在多个基准测试中表现出色,尤其是 DistilQwen2.5-R1-7B 的性能全面超越了其他开源蒸馏模型。为了方便实际应用,这些模型的 Checkpoint 已在 Hugging Face 和 Model Scope 社区中公开,并提供了在阿里云人工智能平台 PAI 上的操作指南。在未来,随着大语言模型和知识蒸馏技术更进一步的发展,我们将推出各种领域、各种规格的 DistilQwen 系列模型,充分促进大语言模型在实际应用中的降本增效。
参考资料
相关发表论文
1. Yuanhao Yue, Chengyu Wang, Jun Huang, Peng Wang. Building a Family of Data Augmentation Models for Low-cost LLM Fine-tuning on the Cloud. COLING 2025
2. Yuanhao Yue, Chengyu Wang, Jun Huang, Peng Wang. Distilling Instruction-following Abilities of Large Language Models with Task-aware Curriculum Planning. EMNLP 2024
技术文章
1. DistilQwen2.5发布:通义千问蒸馏小模型再升级:https://developer.aliyun.com/article/1653842
2. DistilQwen2:通义千问大模型的知识蒸馏实践:https://developer.aliyun.com/article/1633882
3. DistilQwen2蒸馏小模型的训练、评测、压缩与部署实践:https://help.aliyun.com/zh/pai/user-guide/training-evaluation-compression-and-deployment-of-distilqwen2
4. 大语言模型数据增强与模型蒸馏解决方案:https://help.aliyun.com/zh/pai/user-guide/llm-data-enhancement-and-model-distillation-solution
技术交流答疑群
 |